Spanish version
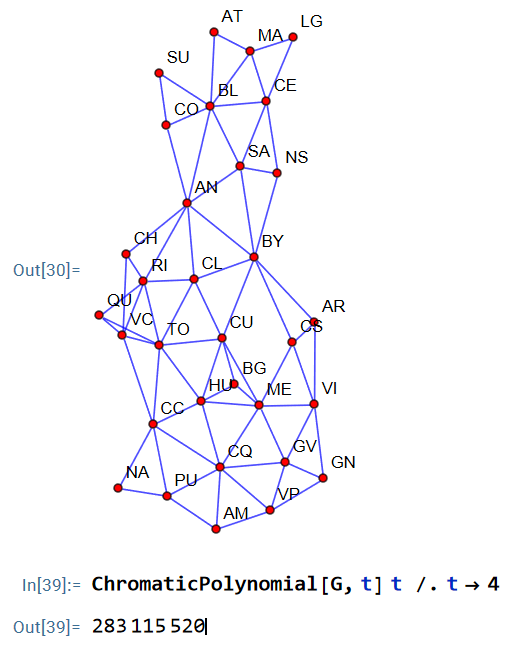
Hola a todxs, desde cualquier parte del mundo. He calculado que el número de formas de colorear el mapa de Colombia sin que dos regiones adyacentes compartan color, usando solamente 4 colores, es:
\[\Large{283\ 115\ 520}\]Cabe anotar que he considerado a Bogotá como un departamento aislado, y el archipiélago de San Andrés y Providencia se pinta de un solo color.
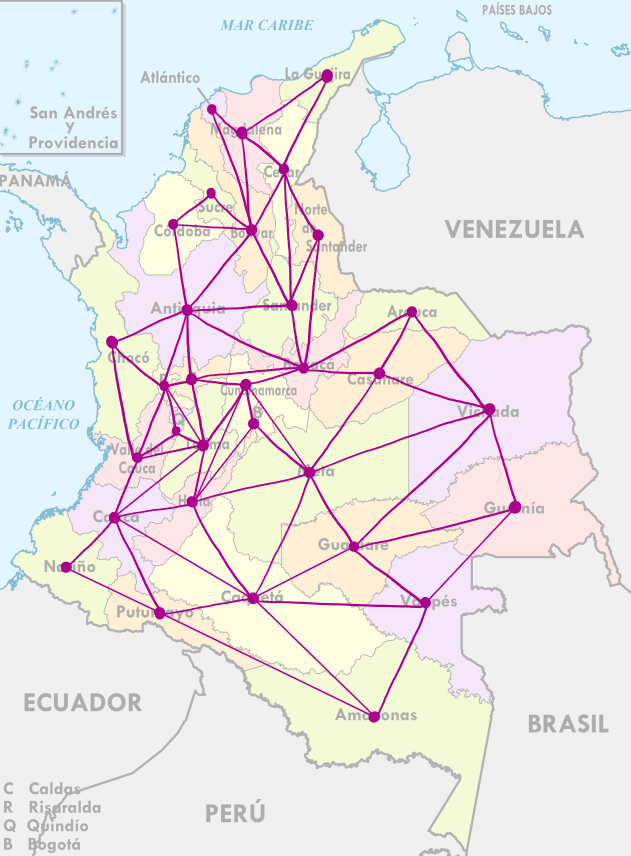
¿Cómo lo he hecho? En Wolfram Mathematica hay un comando muy sencillo que permite calcular el polinomio cromático de cualquier grafo planar. Para quienes no sean conocedores del tema, el problema de colorear un mapa se puede traducir en cómo colorear los vértices de un grafo planar sin que dos vértices adyacentes queden coloreados por el mismo color. Esto lo podemos hacer ya que hay una correspondencia entre ambos objetos si a cada departamento le asignamos un vértice en un grafo, y dibujamos una arista en caso de que dos regiones compartan una frontera cuya longitud sea positiva, es decir, no consideraremos como fronteras aquellas regiones que se toquen en esquinas. Como dato curioso, el único cuatrifinio (cuatro esquinas) de Colombia está en las fronteras de Boyacá, Casanare, Cundinamarca y Meta.
A decir verdad no he hecho nada novedoso, lo más tedioso fue listar todas los departamentos de Colombia y sus fronteras a mano. Una vez hecho esto, el programa hace el resto del trabajo basándose en un teorema muy conocido, llamado el teorema de eliminación-contracción, que dice que si $\chi(G,t)$ representa el número de formas de colorear un grafo $G$ empleando solamente $t$ colores, y si $e$ es una arista del grafo, entonces \(\chi(G, t)=\chi(G-e, t)-\chi(G / e, t),\) donde $G-e$ es el grafo obtenido a partir de quitar la arista $e$, y $G/e$ es el grafo que resulta de juntar los vértices que une $e$ en un solo vértice y si quedan aristas dobles considerarlas como una sola. Es gracias a esta recurrencia que $\chi(G,t)$ es de hecho un polinomio, llamado el polinomio cromático de $G$.
Específicamente, el polinomio cromático de Colombia es
\[\begin{align*} \chi(G_{\text{Col}},t)&=t^{33}-72 t^{32}+2514 t^{31}\\ &\quad-56703 t^{30}+928416 t^{29}-11757140 t^{28}\\ &\quad+119803182 t^{27}-1008989839 t^{26}+7159276765 t^{25}\\ &\quad-43406309014 t^{24}+227281194275 t^{23}-1036142031322 t^{22}\\ &\quad+4137985048853 t^{21}-14543216293518 t^{20}+45128702300210 t^{19}\\ &\quad-123904692011141 t^{18}+301323104920452 t^{17}-649111128011288 t^{16}\\ &\quad+1237494226626151 t^{15}-2083729861163011 t^{14}+3089197236230153 t^{13}\\ &\quad-4014284821039240 t^{12}+4544515915061124 t^{11}-4446080022163760 t^{10}\\ &\quad+3719159851081504 t^9-2622562341468416 t^8+1529179876264320 t^7\\ &\quad-717670769635584 t^6+260520144880896 t^5-68636197988352 t^4\\ &\quad+11673935115264 t^3-961919815680 t^2. \end{align*}\]Todos los detalles formales de $\chi(G,t)$ pueden ser consultados en el artículo [1] donde prueban varias propiedades del polinomio cromático y cuentan cuántas formas hay de colorear los mapas de Canadá, Francia y EEUU.
Este problema crece de forma exponencial gracias a la recurrencia anterior, así que es computacionalmente complejo calcular el polinomio cromático de un grafo si el número de aristas es muy grande. Es por esto que me gustaría, por puro pasatiempo, calcular el polinomio cromático de Colombia usando los teoremas mencionados en el artículo. La forma que por el momento se me ocurre es separar los 3-ciclos en la parte superior del mapa y separar la 6-rueda que proviene del departamento de Santander. También se puede separar el 3-ciclo de Nariño, y tal vez usar el teorema principal de dicho artículo, que permite reducir el polinomio cromático de la intersección de los dos grafos rueda de Caquetá y Guaviare. Sigo pensándolo, pero si alguien más se anima, adelante.
La razón por la que pensé en este problema fue gracias a una conferencia (buenísima) dada por Federico Ardila en el Congreso Colombiano de Matemáticas de 2023 cuando yo era estudiante, en la que nos habló sobre teoría de matroides y sus posibles aplicaciones a la coloración de grafos. Nos motivó a calcular el polinomio cromático de Colombia, nos dijo que le avisáramos una vez lo calculáramos. Pensé que sería muy difícil y por eso lo postergué, pero después de año y medio, aquí está. Avísenle.
Queda a disposición de cualquiera el dataset de las fronteras de Colombia, con esto pueden reconstruir el grafo y calcular otro tipo de objetos interesantes, como su matriz de adyacencia, etc.
¡Saludos!
English version
Hello everyone, from anywhere in the world. I have calculated that the number of ways to color the map of Colombia such that no two adjacent regions share the same color, using only 4 colors, is:
\[\Large{283\ 115\ 520}\]It should be noted that I have considered Bogotá as an isolated department, and the archipelago of San Andrés and Providencia is painted with a single color.
How did I do it? In Wolfram Mathematica, there is a very simple command that allows calculating the chromatic polynomial of any planar graph. For those who are not familiar with the topic, the problem of coloring a map can be translated into how to color the vertices of a planar graph without two adjacent vertices being colored the same. We can do this because there is a correspondence between both objects if we assign a vertex in a graph to each department and draw an edge in case two regions share a boundary with positive length; that is, we will not consider as boundaries those regions that touch at corners. As a curious fact, the only quadrilateral (four corners) in Colombia is at the borders of Boyacá, Casanare, Cundinamarca, and Meta.

To be honest, I have not done anything groundbreaking; the most tedious part was listing all the departments of Colombia and their boundaries by hand. Once this was done, the program does the rest of the work based on a well-known theorem called the deletion-contraction theorem, which states that if $\chi(G,t)$ represents the number of ways to color a graph $G$ using only $t$ colors, and if $e$ is an edge of the graph, then $\chi(G, t)=\chi(G-e, t)-\chi(G / e, t)$, where $G-e$ is the graph obtained by removing the edge $e$, and $G/e$ is the graph that results from merging the vertices connected by $e$ into a single vertex and considering multiple edges as a single edge. It is thanks to this recurrence that $\chi(G,t)$ is indeed a polynomial, called the chromatic polynomial of $G$.

Specifically, the chromatic polynomial of Colombia is
\[\begin{align*} \chi(G_{\text{Col}},t)&=t^{33}-72 t^{32}+2514 t^{31}\\ &\quad-56703 t^{30}+928416 t^{29}-11757140 t^{28}\\ &\quad+119803182 t^{27}-1008989839 t^{26}+7159276765 t^{25}\\ &\quad-43406309014 t^{24}+227281194275 t^{23}-1036142031322 t^{22}\\ &\quad+4137985048853 t^{21}-14543216293518 t^{20}+45128702300210 t^{19}\\ &\quad-123904692011141 t^{18}+301323104920452 t^{17}-649111128011288 t^{16}\\ &\quad+1237494226626151 t^{15}-2083729861163011 t^{14}+3089197236230153 t^{13}\\ &\quad-4014284821039240 t^{12}+4544515915061124 t^{11}-4446080022163760 t^{10}\\ &\quad+3719159851081504 t^9-2622562341468416 t^8+1529179876264320 t^7\\ &\quad-717670769635584 t^6+260520144880896 t^5-68636197988352 t^4\\ &\quad+11673935115264 t^3-961919815680 t^2. \end{align*}\]All the formal details of $\chi(G,t)$ can be consulted in the article [1] where several properties of the chromatic polynomial are proved, and it is counted how many ways there are to color the maps of Canada, France, and the USA.
This problem grows exponentially due to the previous recurrence, so it is computationally complex to calculate the chromatic polynomial of a graph if the number of edges is very large. That is why I would like, purely for fun, to calculate the chromatic polynomial of Colombia using the theorems mentioned in the article. The approach that I currently have in mind is to separate the 3-cycles at the top of the map and to isolate the 6-wheel coming from the department of Santander. One could also separate the 3-cycle of Nariño and perhaps use the main theorem of that article, which allows reducing the chromatic polynomial of the intersection of the two graphs, the wheels of Caquetá and Guaviare. I am still thinking about it, but if anyone else is encouraged, go ahead.
The reason I thought of this problem was thanks to a conference (brilliant!) given by Federico Ardila at the 2023 Colombian Mathematics Congress when I was undergrad, where he talked to us about matroid theory and its possible applications to graph coloring. He encouraged us to calculate the chromatic polynomial of Colombia, telling us to notify him once we computed it. I thought it would be very difficult and thus postponed it, but after a year and a half, here it is. Please let him know.
The dataset of the borders of Colombia is available for anyone; with this, you can reconstruct the graph and calculate other interesting objects, such as its adjacency matrix, etc.
Best regards!
References
-
Checa, Daniel F.. (2024). colombia-coloring: ¿De cuántas formas se puede colorear el mapa de Colombia? / How many ways to color Colombia map? [GitHub Repository]. GitHub. https://github.com/dfcheca/colombia-coloring
-
Milenioscuro. (2015). Colombia, administrative divisions – es – colored (+box) [SVG File]. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Colombia,administrative_divisions-es-colored(%2Bbox).svg
-
Bassett, R., Canizales, J., Chahal, J. S., Fackrell, T., & Rico, V. (2019, August 15). How many ways to color the map of America? (arXiv:1908.05694) [Preprint]. arXiv. https://doi.org/10.48550/arXiv.1908.05694